Let a finite set of points P in the plane be given, with each point assigned a positive real weight. P is called a magic configuration if every line determined by two or more points has the same sum of weights, i.e., the sum of the weights of the points through which each line passes is the same. The problem is to prove or disprove that there are only four essentially distinct magic configurations:
Points in general position, with (e.g.) every point assigned weight 1.
All points collinear.
n-1 points collinear with weight (e.g.) 1, and one point not on that line with weight n-2.
The 7-point configuration shown in Fig. 1, or its projective equivalents.
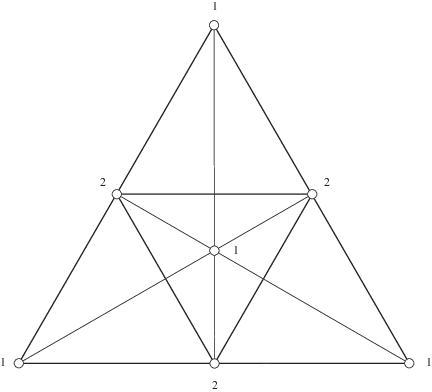
Settled positively, 2007: [ABK+08]
The terminology “magic configuration” comes from the notion of magic squares, 2D matrices such that every row, column, and (optionally) diagonal sums to the same value.
An ordinary line is one that passes through exactly two points. Scaling weights of a magic configuration so that the weights on each line sum to 1, the weight of the points on ordinary lines must be \frac{1}{2} in any magic configuration other than the third example above. It is known that, for n \ge 3 noncollinear points, at least \frac{6}{13} n lines must be ordinary [CS93].
Settled in [ABK+08], the journal version of a paper that originally appeared in the Proceedings of the 2007 Symposium on Computational Geometry.
Originally posed by U. S. R. Murty in [Mur71]. Reposed by Murty at a June 2006 celebration of V. Chvátal’s 60th birthday. Two people who heard this posing, X. Chen and P. Taslakian, brought the problem to the conference Discrete and Computational Geometry—Twenty Years Later in Snowbird, June 2006. In particular, Chen posed the problem at the open-problem session.
point sets
J. O’Rourke, 14 Jul. 2006; E. Demaine, 15 Jul. 2006; J. O’Rourke, 16 Jul. 2008.