Let C be a convex piece of paper; its boundary may be a smooth curve, or a polygon. A perimeter halving folding is a folding of C obtained by identifying two points x and y on the boundary of C that halve the perimeter, and then folding C by “gluing” xy to yx. This always results in a unique convex shape in 3D, a polyhedron if C is a convex polygon [DO07]. What unit-area shape C achieves the maximum volume possible via a perimeter-halving folding?
Posed by Joseph Malkevitch in 2002, in a slightly different form: for polygons, and not restricting the folding to perimeter-halving. The modifications above were suggested at CCCG’05 [DO06]. The restriction to perimeter halving eliminates some more complex foldings possible for some convex polygons, and so in that sense simplifies the problem. The extension to smooth shapes is a natural generalization. Smooth shapes only admit perimeter-halving foldings.
Open.
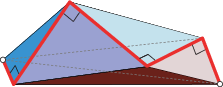
Even fixing the shape and finding the maximum volume perimeter halving for that shape is difficult. For a circular disk, all perimeter halvings lead to a flat doubly-covered half disk, all of volume zero. The only other shape for which the answer is known, and then only empirically, is the case of C a square [ADO03]. The resulting polyhedron of 6 vertices and 8 faces, shown in Fig. 1, achieves about 60% of the volume of a unit-area sphere.
folding and unfolding
J. O’Rourke, 26 Aug. 2005.